Question

Let u and v be distinct vectors of a vector

spaceV. Show that if {u,v} is a basis for V anda
is a non-zero scalar, then {u+v,au} is also abasis for V.

Answer 1

See the proof below.

Explanation:

For this proof we need to begin with the assumption, on this case the vectors u and v are different
`u \\eq v`

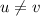
We are assuming that {u,v} is a basis of V and distinct, so then we have that V is a 2 dimensional vector space and we have the following condition:

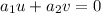`a_1 u + a_2 v =0` if
`a_1 =a_2 = 0` (1)

We need to show that {u+v,au} is also a basis for V, so then we need to show this:

`a_1 (u+v) +a_2 (au) =0`

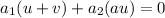
That is equivalent to:

`a_1 u + a_1 v + a_2 au =0`

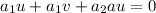
We can take common factor u and we got this:

`(a_1 +a_2 a)u + a_1 v=0`

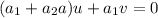
from condition 1 we need to have this:

`a_1 +a_2 a =0 , a \\eq 0`

So then
`a_2 a =0` and
`a_2 =0`

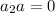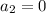
And we will see that
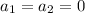`a_1 = a_2 =0` so then we can conclude that {u+v, au} is a linearly independent set of two vectors and are a basis for V.

{u+v, au} is a basis for the space V.