Question

Prove that if {x1x2.......xk}isany

linearly dependent set, then there is at least one
vectorxi in the set that can be expressed as a
linearcombination of the others and conversely.

Answer 1

See the proof below.

Explanation:

What we need to proof is this: "Assuming X a vector space over a scalar field C. Let X= {x1,x2,....,xn} a set of vectors in X, where
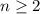`n\geq 2`. If the set X is linearly dependent if and only if at least one of the vectors in X can be written as a linear combination of the other vectors"

Proof

Since we have a if and only if w need to proof the statement on the two possible ways.

If X is linearly dependent, then a vector is a linear combination

We suppose the set
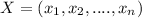`X= (x_1, x_2,....,x_n)` is linearly dependent, so then by definition we have scalars
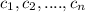`c_1,c_2,....,c_n` in C such that:

`c_1 x_1 +c_2 x_2 +.....+c_n x_n =0`

And not all the scalars
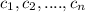`c_1,c_2,....,c_n` are equal to 0.

Since at least one constant is non zero we can assume for example that
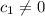`c_1 \\eq 0`, and we have this:

`c_1 v_1 = -c_2 v_2 -c_3 v_3 -.... -c_n v_n`

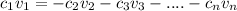
We can divide by c1 since we assume that
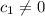`c_1 \\eq 0` and we have this:

`v_1= -(c_2)/(c_1) v_2 -(c_3)/(c_1) v_3 - .....- (c_n)/(c_1) v_n`

And as we can see the vector
`v_1` can be written a a linear combination of the remaining vectors
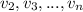`v_2,v_3,...,v_n`. We select v1 but we can select any vector and we get the same result.

If a vector is a linear combination, then X is linearly dependent

We assume on this case that X is a linear combination of the remaining vectors, as on the last part we can assume that we select
`v_1` and we have this:

`v_1 = c_2 v_2 + c_3 v_3 +...+c_n v_n`

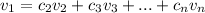
For scalars defined
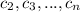`c_2,c_3,...,c_n` in C. So then we have this:

`v_1 -c_2 v_2 -c_3 v_3 - ....-c_n v_n =0`

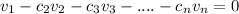
So then we can conclude that the set X is linearly dependent.

And that complet the proof for this case.