Answer:
As the opposite lines have the same slope and are equal in lengths. It is proved that the quadrilateral with given points is indeed a rectangle!
Explanation:
The condition for a quadrilateral to be a rectangle is that
- the opposite lines must be parallel.
- the opposite distances must be equal
Given the points A(2 + √2, −1), B(8 + √2, 3), C(6 + √2, 6), and D(√2, 2)
We don't know in what order they are given, so our first step should be to calculate the distances using the distance formula:
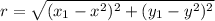
distance AB
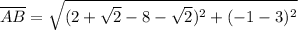

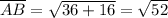
distance BC
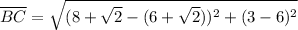
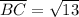
since these two distances are different, the next two SHOULD be equal to AB and BC
distance CD
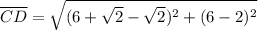
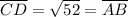
distance DA
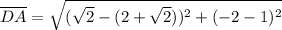
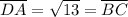
Now we have an idea that since AB = CD and BC = DA, then if this shape is a rectangle then these opposite lines should also be parallel to each other!
Hence we need to see if:
slope of AB = slope of CD
and
slope of BC = slope of DA
to find the slope between two points, we'll use
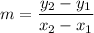
checking: slope of AB = slope of CD:
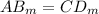
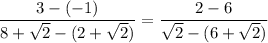
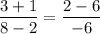
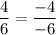
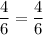
hence the lines AB and CD are parallel and equal!
we can do the same for BC and DA
slope of BC = slope of DA
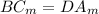
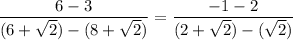
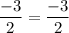
hence the lines BC and DA are parallel and equal as well!