Question

The smaller of two numbers is five less than 1/3 the larger number. Half the larger added to the smaller is 10. Find the numbers.

Answer 1

The numbers are 1 and 18

Solution:

Let the smaller number be "x"

Let the larger number be "y"

Given that smaller of two numbers is five less than
`(1)/(3)` the larger number

smaller number = one - third of larger number - 5

`x = (1)/(3) * y - 5\\\\x = (y - 15)/(3)\\\\`

3x = y - 15

y = 3x + 15 ------- eqn 1

Half the larger added to the smaller is 10

`(1)/(2)y + x = 10\\\\(y + 2x)/(2) = 10`

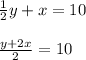
y + 2x = 20 ------- eqn 2

Let us solve eqn 1 and eqn 2

Substitute eqn 1 in eqn 2

3x + 15 + 2x = 20

5x = 20 - 15

5x = 5

x = 1

From eqn 1,

y = 3(1) + 15 = 18

y = 18

Thus the numbers are 1 and 18