Question

A plot of land for sale has a width of x ft. and a length that is 8 ft. less than its width. A farmer will only purchase the

land if it measures 240 ft2. What value for x causes the farmer to purchase the land?

Answer 1

Answer: The value for x causes the farmer to purchase the land should be 20.

Explanation:

Given : A plot of land for sale has a width of x ft. and a length that is 8 ft. less than its width.

i.e. Length of filed = x-8 ft

A farmer will only purchase the land if it measures 240 ft².

i.e. Area should be 240 ft².

Area of field = Length x width

Put values , we get

`\Rightarrow\ 240=(x-8)(x)\\\\\Rightarrow\ 240=x^2-8x\\\\ \Rightarrow\ x^2-8x-240=0\\\\ \Rightarrow\ x^2-8x-240=x^2+12x-20x-240=0\\\\ \Rightarrow x(x+12)-20(x+12)=0\\\\ \Rightarrow(x+12)(x-20)=0\\\\ \Rightarrowx=20\ or\ x=-12`

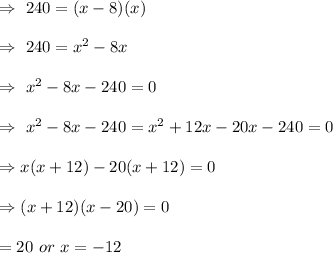
So , x= 20 , width cannot be negative.

Therefore , the value for x causes the farmer to purchase the land should be 20.