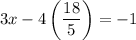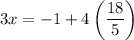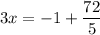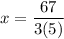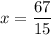Answer:
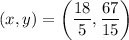
Explanation:
First rearrange all equations into this format:

that will result in:


then we'll multiply an equation with a number such that we have same numbers on both equations (with only different signs). So we can add them
Here you can see that we've multiplied the first equation with (-3) so that we have -9x on one equation and 9x on the other. Now when we add the two equations the 9x and -9x terms will cancel out (or eliminate)
![\[\begin{array}{r@{}l@{\quad}l@{\quad}r@{}l@{}c}3x-4y&{}=-1&\xrightarrow{* (-3)}&-9x +12y&{}=+3\\[\jot]9x -7y&{}=15&\xrightarrow{\phantom{* (-3)}}&9x-y&{}=15&~\smash{\raisebox{.8\\ormalbaselineskip}{$+$}}\\\cline{4-5}&&&+5y&{}=18\\[\jot]&&&y&{}=(18)/(5)\\\end{array}\]\\](https://img.qammunity.org/2021/formulas/mathematics/college/9ll59wt3ws44eh410y3yuyjovz46gua95x.png)
now that we've found the value of y
we'll use this value in any of the two equations to get the value of x.
let's put y in the first equation: