Question

A bacterial culture grows exponentially according to the function n(t)=n(e^rt), where n(t) is the quantity after "t" hours and "n" is the original quantity. If the culture grows from 20 bacteria to 45 bacteria in 2 days, how many bacteria will there be in 5 days?

Answer 1

There will be 152 bacteria in 5 days.

Explanation:

We have that

`n(t) = ne^(rt)`

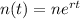
We have that the original quantity is 20. So
`n = 20`

We also have that
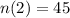`n(2) = 45`. This helps us find r.

`n(t) = ne^(rt)`

`45 = 20e^(2r)`

`e^(2r) = 2.25`

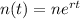
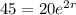
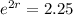
Now we apply ln to both sides

`2r = 0.811`

`r = 0.405`

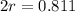
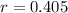
How many bacteria will there be in 5 days?

This is n(5)

`n(t) = ne^(rt)`

`n(5) = 20*e^(5*0.405) = 152`

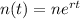
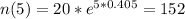
There will be 152 bacteria in 5 days.