Question

The dimensions of a closed rectangular box are measured

as80cm, 60 cm, 50cm, respectively, with a possible error of .2 cm
ineach dimension. Use differentials to estimate the maximumerror in
calculating the surface area of the box.

Answer 1

The maximum error in calculating the surface area of the box is 152 square cm.

Explanation:

We are given the following information in the question:

The dimensions of a closed rectangular box are measured as 80 cm, 60 cm, 50 cm, respectively.

Possible error = 0.2 cm

Surface area of rectangular box =

`S = 2(lb + bh + lh)`

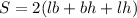
where l, b and h are the length, breadth and height of the rectangular box respectively.

Change in area =

`\Delta S \approx dS = 2(l\Delta b + b\Delta l + b\Delta h + h\Delta b + l\Delta h + h\Delta l)\\`

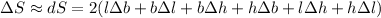
Putting the values, we get,

Change in area =

`=2(\Delta l (b+h) + \Delta b (h+l) + \Deltah(l + b))\\=2(0.2(110) + 0.2(130) + 0.2(140))\\= 152\text{ square cm}`

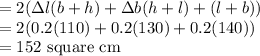
The maximum error in calculating the surface area of the box is 152 square cm.