Answer:
i) -2
Explanation:
In mathematics, Vieta's formulas relate the coefficients of a polynomial to sums and products of its roots.
c and d are solutions(roots) of
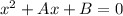
a and b are solutions(roots) of
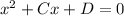
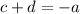 eq. 1
eq. 1
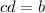 eq. 2
eq. 2
 eq. 3
eq. 3
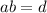 eq. 4
eq. 4
from eq. 1 we get
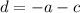
from eq. 3 we get
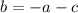
so

now substitute
 in eq. 2
in eq. 2

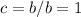
now substitute
 in eq. 4
in eq. 4
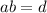
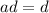
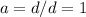
now substitute the values of
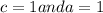 in eq. 1
in eq. 1
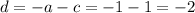
similarly, substitute the values of
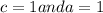 in eq. 3
in eq. 3

Finally,
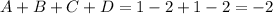
Lets verify and see if our answer is right!
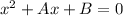
Substituting the values of A and B
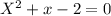
we know that c and d are solutions of this equation so they must satisfy the equation.
put
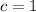
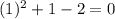

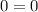 (proved)
(proved)
put

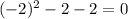
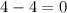
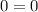 (proved)
(proved)