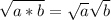Question

A suitcase measures 24 inches long and -8 i aches high. What is the diagonal length of the suitcase? (Pythagorean Theorem)

Answer 1

Diagonal Length =
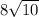`8√(10)` inches

Explanation:

The suitcase is a rectangle with one side being 24 and another side being 8.

The diagonal is the line through the middle connecting two opposite corners.

If we draw the diagonal, it creates a triangle with one leg being 24 and another being 8.

The diagonal is the "hypotenuse" of the triangle.

Now, the pythagorean theorem:

leg^2 + another leg^2 = hypotenuse^2

So, we substitute the values known and find the hypotenuse (which is length of the diagonal). Shown below:

`24^2+8^2=h^2\\640=h^2\\h=√(640)\\h=√(64*10)\\h=√(64)√(10)\\h=8√(10)`

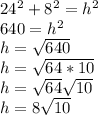
We have written the answer in exact form (with radical in simplified term).

We also use the radical property
`√(a*b)=√(a)√(b)`