Answer:
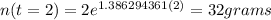
So then after 2 hours we will have 32 grams.
Explanation:
For this case we have the followin exponential model:
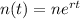
n(t) is the quantity after t hours, n is the original quantityand t represent the hours and r the rate constant.
For this case we know that n(0) = 2 grams and n(3) = 128 grams and we want to find n(2)=?
From the initial condition we know that n = 2, and we have the model like this:
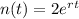
Now if we apply the other conditionn(3) = 128 we got:

If we divide both sides by 2 we got:
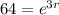
If we apply natural log for both sides we got:
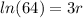
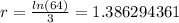
And our model is this one:
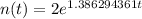
And if we replace t = 2 hours we got:
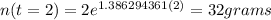
So then after 2 hours we will have 32 grams.