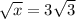Answer:
a)
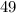
b)
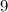
c)
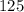
d)
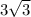
Explanation:
a. Evaluate x^2 when x = 7.
saying
 is the same as saying
is the same as saying
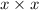
so, when
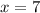 , it means
, it means

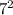

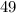
b. Evaluate √x when x = 81.
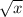 is the opposite of
is the opposite of
 . It shows that, if there's a number 81, then what number multiplied with itself twice to make 81?
. It shows that, if there's a number 81, then what number multiplied with itself twice to make 81?
----------
More generally, if there's a number
 then the square root shows that the number
then the square root shows that the number
 multiplied with itself twice to make
multiplied with itself twice to make
 . Hence
. Hence
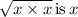
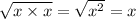
------------
we know that
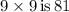
we can write
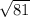
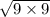
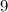
c. Evaluate x^3 when x = 5.
Just as
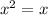
similarly,
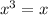 ,
,
so when x=5.
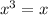
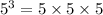
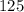
d. Evaluate √x when x = 27.
We know that
 ,
,
we also know that
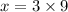
we break this further
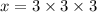
the square root takes shows the number that multiples with itself twice
Here we 3 multiplying itself three times within the square root!
but no worries, we're only going to take two 3's from here.

we're only going to select two 3's within the square root and reveal the answer.
another to think about this is:
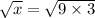
9 is a number that is 3 x 3 hence
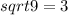
so our answer will be: