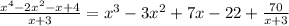Question

If h(x)=x^4-2x^2-x+4 , then what is h(x)/(x+3)? You may use either long or synthetic division.

Answer 1

`(x^4\:-\:2\:x^2\:-\:x\:+\:4)/(x\:+\:3)=x^3-3x^2+7x-22+(70)/(x+3)`

Explanation:

We are going to use long division to find the expression for
`(x^4\:-\:2\:x^2\:-\:x\:+\:4)/(x\:+\:3)`

Step 1: Divide
`(x^4-2x^2-x+4)/(x+3)`

• Divide the leading coefficients of the numerator
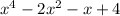  `x^4-2x^2-x+4` and the divisor
  `x+3`

`(x^4)/(x)=x^3`

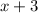
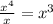
Quotient =
`x^3`

• Multiply
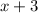  `x+3` by
  `x^3`

`x^4+3x^3`

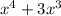
• Subtract
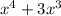  `x^4+3x^3` from
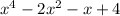  `x^4-2x^2-x+4` to get new remainder

Remainder =
`-3x^3-2x^2-x+4`

Therefore,

`(x^4-2x^2-x+4)/(x+3)=x^3+(-3x^3-2x^2-x+4)/(x+3)`

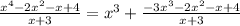
Step 2: Divide
`(-3x^3-2x^2-x+4)/(x+3)`

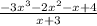
Quotient =
`-3x^2`

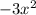
Remainder =
`7x^2-x+4`

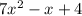
Therefore,

`(x^4-2x^2-x+4)/(x+3)=x^3-3x^2+(7x^2-x+4)/(x+3)`

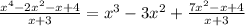
Step 3: Divide
`(7x^2-x+4)/(x+3)`

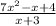
Quotient =
`7x`

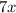
Remainder =
`-22x+4`

Therefore,

`(x^4-2x^2-x+4)/(x+3)=x^3-3x^2+7x+(-22x+4)/(x+3)`

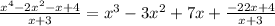
Step 4:

Quotient =
`-22`

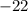
Remainder =
`70`

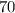
Therefore,

`(x^4-2x^2-x+4)/(x+3)=x^3-3x^2+7x-22+(70)/(x+3)`