Answer:
After 9 years, the population reach 4000.
Explanation:
The given function P(t) represents the size of a small herbivore population at time t (in years).

We need to find the number of years after which population reach 4000.
Substitute P(t)=4000 in the above function.

Divide both sides by 1000.
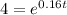
Taking ln on both sides.
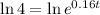
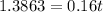
![[\because \ln e^x=x]](https://img.qammunity.org/2021/formulas/mathematics/college/vipbvpu1rckd52lzb22wdf5f2q4dwd380t.png)
Divide both sides by 0.16.
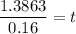
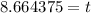
We need to find the number of years. So, round the answer to the next whole number.
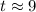
Therefore, after 9 years, the population reach 4000.