Question

The height of Stephanie's kite above the ground is 11 feet less than twice the distance from stepahnie, who is flying the kite to a point below it.Stephanie has let out 53 feet of string to the kite. How high is the kite?

Answer 1

45 feet

Explanation:

Let x be the distance of Stephanie from the point on the ground

Height of kite=
`2x-11`

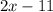
Length of string=53 feet

Pythagoras theorem

`(Hypotenuse)^2=(Base)^2+(Perpendiculars\;side)^2`

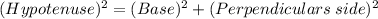
By using Pythagoras theorem

`AC^2=AB^2+BC^2`

`(53)^2=x^2+(2x-11)^2`

`x^2+4x^2+121-44x=2809`

`5x^2-44x+121-2809=0`

`5x^2-44x-2688=0`

`5x^2-140x+96x-2688=0`

`5x(x-28)+96(x-28)=0`

`(x-28)(5x+96)=0`

`x-28=0\implies x=28`

`5x+96=0`

`5x=-96`

`x=-(96)/(5)`

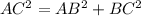
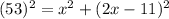
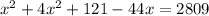
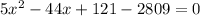
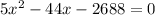
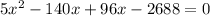
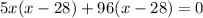
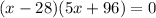
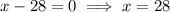
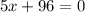
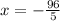
It is not possible because distance cannot be negative.

x=28 feet

Substitute the value of x

Height of kite above the ground=2(28)-11=45 feet

Therefore,height of kite from the ground=45 feet