Question

A metal conduit will be used as a pathway for wiring through a concrete block. The conduit is a 5 foot long rod with an outer diameter of 2 inches and an inner diameter of 1.8 inches. What is the volume of metal in the conduit in cubic centimeters?

Answer 1

Answer: 586.59 cubic centimeters .

Explanation:

As per given . we have

Inner diameter = 1.8 inches

⇒Inner radius :r = 0.9 in. (radius is half of diameter)

= 0.9 x (2.54) = 2.286 cm [∵ 1 in . = 2.54 cm]

Outer diameter = 2 inches

⇒Outer radius : R = 1 inch = 2.54 cm

Height : h = 5 feet = 5 x(30.48) = 152.4 cm [∵ 1 foot = 30.48 cm]

The formula to find the volume of a hollow cylinder :

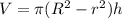`V=\pi(R^2-r^2)h` , where R= outer radius , r= inner radius and h= height.

Now , the volume of metal in the conduit :

`V=(3.14)(( 2.54)^2-(2.286)^2)(152.4)`

`V=(3.14)(6.4516-5.225796)(152.4)`

`V=(3.14)(1.225804)(152.4)`

`V=586.591342944\approx586.59\ cm^3`

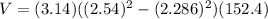
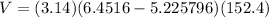
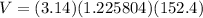
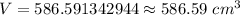
Hence, the volume of metal in the conduit is 586.59 cubic centimeters .