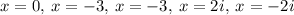Answer:
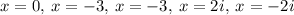
Explanation:
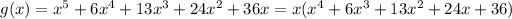
We have a zero at x = 0.
Possible rational zeros: (highest and lowest power's coefficients)
36 ⇒ 1, 2, 3, 4, 6, 9, 12, 18, 36
1 ⇒ 1
+ {1, 2, 3, 4, 6, 9, 12, 18, 36} and - {1, 2, 3, 4, 6, 9, 12, 18, 36}
f(-3) = 81 - 162 + 117 - 72 + 36 = 0
So, (x+3) is a factor.
Here comes the synthetic division part that I have shown in the attachment.
As shown in the attachment the function has double zeros at x = -3.
After synthetic division, the remaining part is
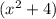
It also means that we have 2 complex zeros at x = 2i and x=-2i
So the final form of g(x) is
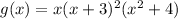
Final solution is