Answer:
a)
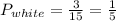
b)
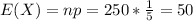
So then we expect to see 50 times the white ball out of the 250 trials for the experiment.
Explanation:
Previous concepts
The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".
Solution the problem
For this case have 3 White, 8 red, 2 blue and 2 yellow
So the total number of balls in the bag are 3+8+2+2=15
The experiment consist in take 1 ball and put it back. So is a experiment with replacement. And for each trial the individual probabilities for each color are:
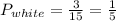
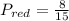
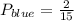
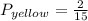
Part a
For this case the probablity that Casey choses a white ball is always the same and is:
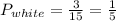
Part b
For this case we repeat the experiment 250 times and we want to find how many times we expect that Casey will choose the white ball. We can assume that our random variable X who represent "The number of white balls selected" is a binomial experiment.
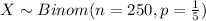
And the expected value is given by this expression:
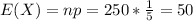
So then we expect to see 50 times the white ball out of the 250 trials for th experiment.