Question

Evaluate the integral (3 - 2x)dx for x = -1 to x = 3
byinterpreting it in terms of areas.

Answer 1

4 unit^2

explanation is given at the end.

Explanation:

What this integral represents is the net area between the function f(x) = 3 - 2x

and the x-axis, between the range of x between -1 and 3.

`\int^(3)_(-1) {3-2x} \, dx \\\left|3x - 2(x^2)/(2)\right|^(3)_(-1)\\\left|3x - x^2\right|^(3)_(-1)`

we have integrated the equation, and now we're going to put the limits find the area under the function f(x)

`\left|3x - x^2\right|^(3)_(-1)\\(3(3)-(3)^2)-(3(-1)-(-1)^2)`

-------------

if these seems like a big jump, try to understand it through this:

`\left|3x - x^2\right|^(b)_a\\(3(b)-(b)^2)-(3(a)-(a)^2)\\`

we've only distributed the limits each time to the same integrated expression.

--------------

coming back to our solution:

`(3(3)-(3)^2)-(3(-1)-(-1)^2)`

`(0)-(-4)`

`4`

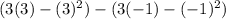
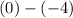
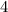
so our area is 4

the area above the x-axis is positive, and the area below the x-axis is negative. Since, our answer is +4. We now know that if within this range [-1,3] the area above and below the x-axis exist, there is more area above the x-axis than below the x-axis. In other words, the net area is above the x-axis and that is equal to 4 unit^2