Answer:
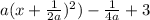
Explanation:
We have been given an expression
 . We are asked to complete the square for the given expression.
. We are asked to complete the square for the given expression.
First of all, we will factor our a as:
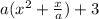
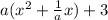
Now, we need to add and subtract half the square of the middle term, that is
 :
:
![a[x^2+(1)/(a)x+((1)/(2a))^2-((1)/(2a))^2]+3](https://img.qammunity.org/2021/formulas/mathematics/high-school/18sq1kkzf0aun0e4eqk0uojgoe9xz2ry7e.png)
![a[x^2+(1)/(a)x+((1)/(2a))^2-((1)/(4a^2))]+3](https://img.qammunity.org/2021/formulas/mathematics/high-school/o27p0j61aumnljhws8xh6lfral6xtbh16k.png)
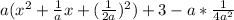
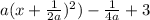
Therefore, our required square would be
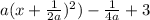 .
.