Question

A particle moves in a straight line so that its velocity at time

tis v(t) = t3. If its position at time t is s(t) and
s(1)= 2, find s(2).

Answer 1

s(2) = 7.75

Explanation:

given the velocity v(t) = t^3

we can find the position s(t) by simply integrating v(t) and using the boundary conditions s(1)=2

`s(t) = \int {v(t)} \, dt\\ s(t) = \int {t^3} \, dt\\s(t) = (t^4)/(4)+c`

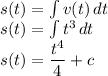
we know throught s(1) = 2, that at t=1, s =2. we can use this to find the value of the constant c.

`s(1) = (1^4)/(4)+c\\4 = (1^4)/(4)+c\\c = 4-(1)/(4)\\c = (15)/(4) = 3.75`

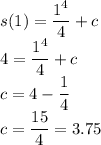
Now we can use this value of t to formulate the position function s(t):

`s(t) = (t^4)/(4)+(15)/(4)\\`

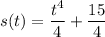
this is the position at time t.

to find the position at t=2

`s(2) = (2^4)/(4)+(15)/(4)\\`

`s(2) = (2^4)/(4)+(15)/(4)\\`

`s(2) = (31)/(4) = 7.75`

the position of the particle at time, t =2 is s(2) = 7.75