Question

You walk from point A 8 miles due north, then 5 miles dues east, and then 4 miles due north to point B. How far is point A from point B on a straight line?

Answer 1

Point A is
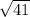`√(41)` miles far from point B.

Explanation:

Draw a diagram by using the given information.

1. Move 8 units up to reach at point Q. (Walk from point A ,8 miles due north).

2. Move 5 units right to reach at point R. (5 miles dues east)

3. Move 4 units down to reach at point B. (4 miles due north to point B)

4. Drawn a line PB as shown below.

From the below figure it is clear that

AP = 8-4 = 4 miles

PB = QR = 5 miles

Using Pythagoras we get

`hypotenuse^2=perpendicular^2+base^2`

`AB^2=AP^2+PB^2`

`AB^2=4^2+5^2`

`AB^2=41`

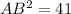
Taking square root on both sides.

`AB=√(41)`

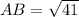
Therefore, point A is
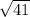`√(41)` miles far from point B.