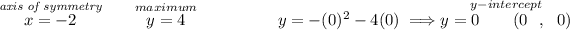Question

This is also something that I don't know!

Answer 1

so the coefficient of the leading term namely x² is negative, meaning is a vertical parabola that's upside-down, kinda like the parabola in the picture below, the axis of symmetry is simply the x-coordinate of the vertex, where if we were to put a mirror there, the other side gets reflected on the mirror, axis of symmetry or the line where the twins split.

to get the y-intercept we simply set x = 0 and solve for "y", is where the graph touches the y-axis and that only happens when "x" reaches 0.

`\textit{vertex of a vertical parabola, using coefficients} \\\\ y=\stackrel{\stackrel{a}{\downarrow }}{-1}x^2\stackrel{\stackrel{b}{\downarrow }}{-4}x\stackrel{\stackrel{c}{\downarrow }}{+0} \qquad \qquad \left(-\cfrac{ b}{2 a}~~~~ ,~~~~ c-\cfrac{ b^2}{4 a}\right) \\\\\\ \left(-\cfrac{ -4}{2(-1)}~~~~ ,~~~~ 0-\cfrac{ (-4)^2}{4(-1)}\right)\implies \left( -2~~,~~0-\cfrac{16}{-4} \right)\implies (\stackrel{x}{-2}~~,~~\stackrel{y}{4}) \\\\[-0.35em] ~\dotfill`

`\stackrel{\textit{axis of symmetry}}{x = -2}\qquad \stackrel{maximum}{y = 4}~\hfill y=-(0)^2-4(0)\implies\stackrel{y-intercept}{ y=0\qquad (0~~,~~0)}`