Answer:
e)
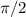
f)
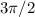
g)
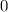
h)

i)
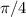
j)
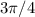
Explanation:
We can solve this exercise by watching a basic trigonometric table
Here i will list values of sin and cos in the points
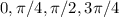 and
and

Hence, the sin takes the value 1 on
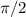 , while it takes the value -1 in its opposite value - \pi/2 (because it is an odd function). If we use the periodicity of the sin, then sin(- \pi/2 + 2 \pi) = -1. Hence
, while it takes the value -1 in its opposite value - \pi/2 (because it is an odd function). If we use the periodicity of the sin, then sin(- \pi/2 + 2 \pi) = -1. Hence
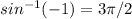
The cos takes value 1 in 0, and it takes the value -1 in

The tangent is the quotient between sin and cos. The tangent is 1 when both cos and sin are equal. We can see that they are equal in
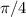 , where they take the value
, where they take the value
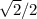
The tangent is -1 where they are the opposite. This happens in
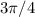 where they take the value
where they take the value
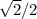 and
and
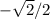 respectively.
respectively.