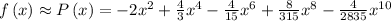Answer:
The Maclaurin of
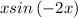 is
is
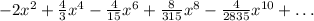 .
.
Explanation:
Taylor series of function
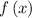 at a is defined as:
at a is defined as:
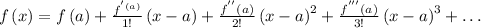
Maclaurin series of function
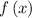 is a Taylor series of function
is a Taylor series of function
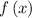 at a = 0
at a = 0
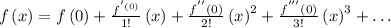
Step 1: Find the derivatives of
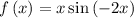 at a = 0
at a = 0
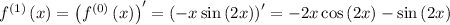
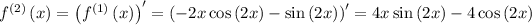
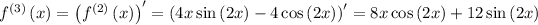
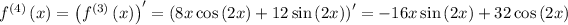
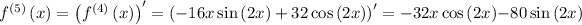
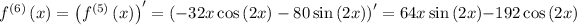
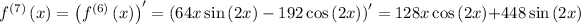
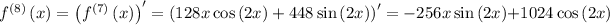
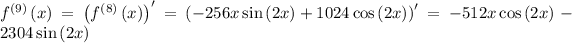
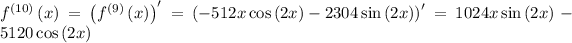
Step 2: Evaluate the derivatives at the given point.
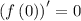
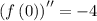
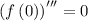
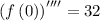
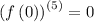
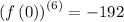
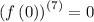
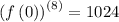
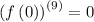
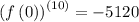
Step 3: Use the calculated values to get a polynomial
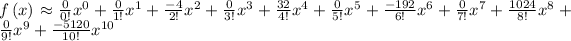
Simplify,