Question

Example 1: Calculation of Normal Probabilities Using ????????-Scores and Tables of Standard Normal Areas The U.S. Department of Agriculture (USDA), in its Official Food Plans

(www.cnpp.usda.gov), states that the average cost of food for a 14- to 18-year-old male (on the Moderate-Cost Plan) is $261.50 per month. Assume that the monthly food
cost for a 14- to 18-year-old male is approximately normally distributed with a mean of $261.50 and a standard deviation of $16.25.
a. Use a table of standard normal curve areas to find the probability that the monthly food cost for a randomly selected 14- to 18-year-old male is
i. Less than $280.
ii. More than $270.
iii. More than $250.
iv. Between $240 and $275.
b. Explain the meaning of the probability that you found in part (a)(iv).

Answer 1

i) 0.872

ii) 0.300

iii) 0.76

iv) 0.704

Explanation:

We are given the following information in the question:

Mean, μ = $261.50 per month

Standard Deviation, σ = $16.25

We are given that the distribution of monthly food cost for a 14- to 18-year-old male is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

a) P(Less than $280)

`P( x < 280) = P( z < \displaystyle(280 - 261.50)/(16.25)) = P(z< 1.138)`

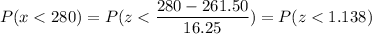
Calculation the value from standard normal z table, we have,

`P(x < 280) = 0.872 = 87.2\%`

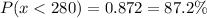
b) P(More than $270)

P(x > 270)

`P( x > 270) = P( z > \displaystyle(270 - 261.50)/(16.25)) = P(z > 0.523)`

`= 1 - P(z \leq 0.523)`

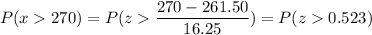
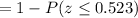
Calculation the value from standard normal z table, we have,

`P(x > 270) = 1 - 0.700 = 0.300 = 30.0\%`

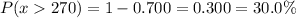
c) P(More than $250)

P(x > 250)

`P( x > 250) = P( z > \displaystyle(250 - 261.50)/(16.25)) = P(z > -0.707)`

`= 1 - P(z \leq -0.707)`

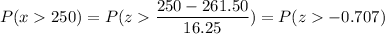
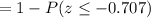
Calculation the value from standard normal z table, we have,

`P(x > 250) = 1 - 0.240 = 0.76 = 76.0\%`

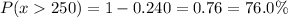
d) P(Between $240 and $275)

`P(240 \leq x \leq 275) = P(\displaystyle(240 - 261.50)/(16.25) \leq z \leq \displaystyle(275-261.50)/(16.25)) = P(-1.323 \leq z \leq 0.8307)\\\\= P(z \leq 0.8307) - P(z < -1.323)\\= 0.797 - 0.093 = 0.704 = 70.4\%`

`P(240 \leq x \leq 275) = 70.4\%`

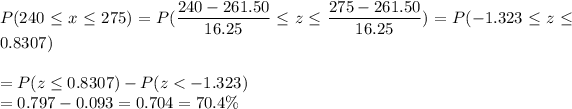
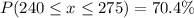
e) Thus, 0.704 is the probability that the monthly food cost for a randomly selected 14- to 18-year-old male is between $240 and $275.