Answer:
See proof below
Explanation:
We have to verify that if we substitute
 in the equation
in the equation
 the equality is true.
the equality is true.
Let's substitute first in the right hand side:
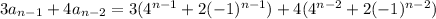
Now we use the distributive laws. Also, note that
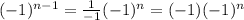 (this also works when the power is n-2).
(this also works when the power is n-2).
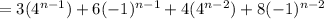

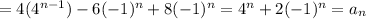
then the sequence solves the recurrence relation.