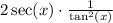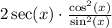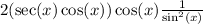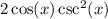Answer:
Proof in explanation.
Explanation:

I'm going to find a way to combine the fractions as one.
Multiply the first fraction by
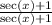 and multiply the second fraction by
and multiply the second fraction by
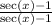 .
.
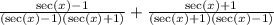
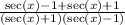
The bottom product can easily be determine since when multiplying the conjugate of
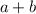 which
which
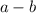 , we only have to multiply first terms and then last terms giving us
, we only have to multiply first terms and then last terms giving us
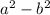 .
.
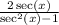
Recall the Pythagorean Identity:

So I can replace
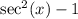 with
with
 :
: