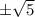Question

Find all the zeros for each function P(x)=x^4-4x^3-x^2+20x-20

Answer 1

The zeros of the given polynomial function are

2,2,
`\pm√(5)`

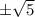
Explanation:

Given polynomial is
`P(x)=x^4-4x^3-x^2+20x-20`

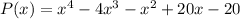
To find the zeros equate the given polynomial to zero

ie., P(x)=0

`P(x)=x^4-4x^3-x^2+20x-20=0`

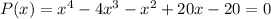
By using synthetic division we can solve the polynomial:

2_| 1 -4 -1 20 -20

0 2 -4 -10 20

_____________________

1 -2 -5 10 |_0

Therefore x-2=0

x=2 is a zero of P(x)

Now we can write the cubic equation as below:

`x^3-2x^2-5x+10=0`

Again using synthetic division

2_| 1 -2 -5 10

0 2 0 -10

______________

1 0 -5 |_0

Therefore x-2=0

x=2 is also a zero of P(x).

Now we have
`x^2+0x-5=0`

`x^2-5=0`

`x^2=5`

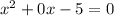
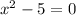
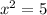
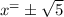`x^=\pm√(5)` is a zero of P(x)

Therefore the zeros are 2,2,
`\pm√(5)`