Question

A circular swimming poolwith a diameter of 28 feet has

a deck ofuniform width built around it. If the area of the deckis
60(pi) square feet,find its width.

Answer 1

2 feet

Explanation:

Let 'w' be twice the width of the deck.

The area of the swimming pool is:

`A_p = (\pi d^2)/(4)\\A_p = (\pi 28^2)/(4) = 196\pi\\`

The area of the swimming pool plus the deck is:

`A_(p+d) = (\pi (d+w)^2)/(4)\\`

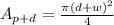
Therefore, the area of the deck is given by:

`A_d = A_(p+d) - A_p\\A_d = 60\pi = (\pi (28+w)^2)/(4) - 196\pi\\1,024 = (28+w)^2\\w^2+56w - 240 = 0`

Solving the quadratic equation:

`w^2+56w - 240 = 0\\w= -56 \pm(√(56^2-(4*1*-240)) )/(2) \\w_1 = -60\\w_2 = 4`

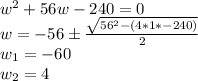
Since the width cannot be negative, w = 4 feet, ad the width is 2 feet.