Question

A club sells 1000 raffle tickets for a brand new

laptopcomputer worth $1500. If each raffle ticket costs $5, then
find theexpected value of the purchase of one ticket. Waht is the
smallestpurchase price for which the club will not lose any
money?

Answer 1

EV = -$3.50

Price = $1.50

Explanation:

By purchasing one ticket, a person has a 1 in 1000 probability of winning the laptop computer worth $1,500 (with a value of $1,495 discounting the ticket price) and a 999 in 1000 probability of losing $5. The expected value is:

`EV = (1)/(1000)*1495 -((999)/(1000)*5)\\EV = -\$3.50`

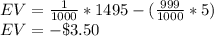
The expected value of the purchase of one ticket is -$3.50.

In order for the club to not lose any money, the total cost of the 1000 tickets must equal the value of the computer:

`P = (\$1,500)/(1,000)\\P=\$1.50`

The smallest purchase price for which the club will not lose any money IS $1.50