Question

Suppose that a computer software company has 30

programmers.Use factorials to write the number of different ways
they couldselect a group of 6 of the programmers to work on a
particularproject.

Answer 1

Answer:
`(30!)/(6!(24)!)`

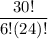
Explanation:

Given : The total number of programmers in the company = 30

The company wants to select a group of 6 programmers to work on a particular project.

Since the order of selecting them does not matters , therefore we use combinations.

The number of combinations of r things taken from n things is given by :-

`^nC_r=(n!)/(r!(n-r)!)`

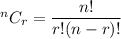
here, n= 30 and r= 6

So the number of different ways to form they could select a group of 6 would be
`^(30)C_(6)=(30!)/(6!(30-6)!)`

`=(30!)/(6!(24)!)\\\\=(30*29*28*27*26*25*24!)/((720)24!)=593775`

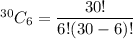
i.e. Total ways =593775

In terms of factorials , the number of total ways to form they could select a group of 6 is
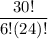`(30!)/(6!(24)!)` .