Question

It appears that people who are mildly obese are less active than leaner people. One study looked at the average number of minutes per day that people spend standing or walking. among mildly obese people, the mean number of minutes of daily activity (standing or Walking) is approximately Normally distributed with the mean 373 minutes and standard deviation 67 minutes. the mean number of minutes of daily activity for lean people is approximately Normally distributed with mean 526 minutes and standard deviation 107 minutes. A researcher records the minutes of activity for an SRS of 5 mildly obese people and an SRS of 5 lean people.

A) What is the probability that the mean number of minutes of daily activity of the 5 mildly obese people exceeds 420 minutes?
B) What is the probability that the mean number of minutes of daily activity of the 5 lean people exceeds 420 minutes?

Answer 1

a) 10.93% probability that the mean number of minutes of daily activity of the 5 mildly obese people exceeds 420 minutes.

b) 99.22% probability that the mean number of minutes of daily activity of the 5 lean people exceeds 420 minutes.

Explanation:

The Central Limit Theorem estabilishes that, for a random variable X, with mean
`\mu` and standard deviation
`\sigma`, a large sample size can be approximated to a normal distribution with mean
`\mu` and standard deviation
`(\sigma)/(√(n))`.

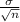Normal probability distribution

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Mildly obese

Normally distributed with mean 373 minutes and standard deviation 67 minutes. So
`\mu = 373, \sigma = 67`

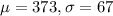
A) What is the probability that the mean number of minutes of daily activity of the 5 mildly obese people exceeds 420 minutes?

So
`n = 5, s = (67)/(√(5)) = 29.96`

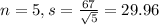
This probability is 1 subtracted by the pvalue of Z when X = 410.

`Z = (X - \mu)/(s)`

`Z = (410 - 373)/(29.96)`

`Z = 1.23`

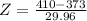
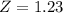
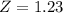`Z = 1.23` has a pvalue of 0.8907.

So there is a 1-0.8907 = 0.1093 = 10.93% probability that the mean number of minutes of daily activity of the 5 mildly obese people exceeds 420 minutes.

Lean

Normally distributed with mean 526 minutes and standard deviation 107 minutes. So
`\mu = 526, \sigma = 107`

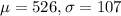
B) What is the probability that the mean number of minutes of daily activity of the 5 lean people exceeds 420 minutes?

So
`n = 5, s = (107)/(√(5)) = 47.86`

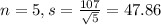
This probability is 1 subtracted by the pvalue of Z when X = 410.

`Z = (X - \mu)/(s)`

`Z = (410 - 526)/(47.86)`

`Z = -2.42`

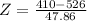
`Z = -2.42` has a pvalue of 0.0078.

So there is a 1-0.0078 = 0.9922 = 99.22% probability that the mean number of minutes of daily activity of the 5 lean people exceeds 420 minutes.