Question

For the function y=x^2-4x-5, perform the followingtasks:

a. put the function in the form y=a(x-h)^2+k. (showwork)
b. what is the equation for the line of symmetry for the
graphof this function?

Answer 1

a.
`x^2-4x-5= \left(x-2\right)^2-9`.

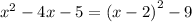b. The axis of symmetry for
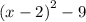`{\left(x - 2\right)^(2)} - 9` is
`x=2`.

Explanation:

a. The vertex form of a quadratic is given by
`y=a(x-h)^2+k`, where (h, k) is the vertex.

To convert from
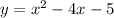`y=x^2-4x-5` form to vertex form you use the process of completing the square.

Step 1: Write
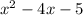`x^2-4x-5` in the form
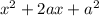`x^2+2ax+a^2`. Add and subtract 4:

`x^(2) - 4 x - 5=x^(2) - 4 x + {\left(4\right)} - {4} - 5`

Step 2: Complete the square
`x^2+2ax+a^2=\left(x+a\right)^2`

`{\left(x^(2) - 4 x + 4\right)} - 9={\left(x - 2\right)^(2)} - 9`

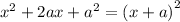
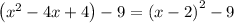
b. The graph of a quadratic function is a parabola. The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves. The axis of symmetry always passes through the vertex of the parabola. The x-coordinate of the vertex is the equation of the axis of symmetry of the parabola.

For a quadratic function in standard form,
`y=a(x-h)^2+k`, the axis of symmetry is
`x=h`.

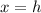The axis of symmetry for
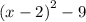`{\left(x - 2\right)^(2)} - 9` is
`x=2`.

Look at the graph shown below.