Answer:
The equations of the two tangents are
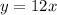 and
and
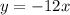 .
.
Explanation:
The given curve is
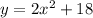 .... (1)
.... (1)
Let the point of tangency is at (a,b).
 .... (2)
.... (2)
Differentiate (1) with respect to x.
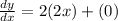
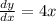
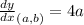
The slope of tangent is 4a.
It is given that tangent passes through the point (a,b) with slope 4a. So, equation of tangent is

where, m is slope.
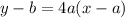 ... (3)
... (3)
The line passes through the point (0,0).
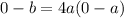
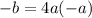
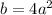 .... (4)
.... (4)
From (1) and (4) we get
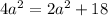
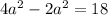

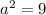
Taking square root on both sides.
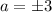
Substitute
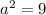 in equation (4).
in equation (4).
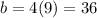
The points of tangency are (3,36) and (-3,36).
Substitute the value of a and b in equation (3) to find the equations of tangents.
For (3,36),
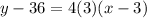
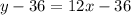
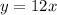
For (-3,36),
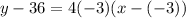
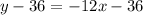
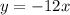
Therefore, the equations of the two tangents are
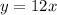 and
and
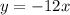 .
.