Question

Prove : the graphs of the function f(x)=x4

and g(x)=x3-x2 have aunique intersection
point.

Answer 1

The unique intersection point for the given functions which is at x = 0.

The intersection point is (0,0)

Explanation:

We are given the following information in the question.

`f(x) = x^4\\g(x) = x^3-x^2`

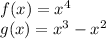
We have to find the intersection point.

Equating the two equations we get,

`x^4 = x^3 - x^2\\x^4 - x^3 + x^2 = 0\\x^2(x^2-x +1) = 0\\x^2 =0, x^2-x +1 = 0\\x = 0, x = 0, x^2-x +1=0`

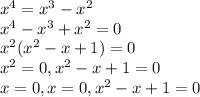
Since the quadratic equation gives complex root, thus there is a unique intersection point for the given functions which is x = 0.

The attached image shows the graph for the given function.

The red line represent f(x) and blue line represent g(x).

The intersection point is (0,0)