Answer: 0.9746
Explanation:
Given : A normally distributed population has a mean of 250 pounds and a standard deviation of 10 pounds.
i.e.

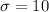
Sample size : n= 20
Let
 sample mean values.
sample mean values.
Then, the probability that this sample will have a mean value between 245 and 255 be
![P(245<\overline{x}<255) =P((245-250)/((10)/(√(20)))<\frac{\overline{x}-\mu}{(\sigma)/(√(n))}<(255-250)/((10)/(√(20))))\\\\=P(-2.236<z<2.236)\ \ [\because \ z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}]\\\\=P(z<2.236)-P(z<-2.236)\\\\=P(z<2.236)-(1-P(z<2.236))\ \ [\because P(Z<-z)=1-P(Z<z)]\\\\=2P(z<2.236)-1\\\\= 2( 0.9873)-1\ \ [\text{By z-table}]\\\\=0.9746](https://img.qammunity.org/2021/formulas/mathematics/college/tuedw3qoj5oajfkhdaz91iatxi5b2vbmw7.png)
Hence , the probability that this sample will have a mean value between 245 and 255 is 0.9746 .