Answer:
sin 77° > cos 77°
Explanation:
The cosine of 77 degree,
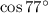
The sine of 77 degree,
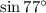
In I quadrant sine and cosine both positive.
But sine is increasing curve and cosine is decreasing curve.
The intersection of sine and cosine at 45°
sin 45° = cos 45°
After intersection, if angle is increasing the value of sine is more than cosine.
- sin 77° > sin 45° ( because sine is increasing)
- cos 77° < cos 45° ( because cosine is decreasing )
But sin 45° = cos 45°
Therefore, sin 77° > cos 77°
Hence, sine of 77 degree is larger than cosine 77 degree.