Answer:
Perimeter would be 23.57 ft ( approx)
Explanation:
Consider triangle ABC is an isosceles triangle,
In which AB = AC,
And, m∠A = 150°,
∵ AB = AC ⇒ m∠B = m∠C,
Now sum of all interior angles of a triangle is 180°,
i.e. m∠A + m∠B + m∠C = 180°,
150°+ m∠B + m∠B= 180°,
2m∠B + 150° = 180°
2m∠B = 30°
⇒ m∠B = 15°
Let D ∈ BC such that AD ⊥ BC,
∵ Altitude of an isosceles triangle is its median,
i.e, BD = DC or BD =
 BC
BC
In triangle ADB,
tan 15° =
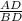
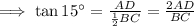
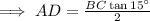 .............(1)
.............(1)
Now, area of triangle ABC =
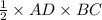
If area = 9 square ft,
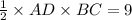
From equation (1),
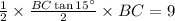
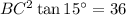
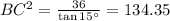
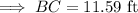
From equation (1),

Using Pythagoras theorem,
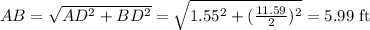
Hence, perimeter of the triangle ABC= AB + BC + CA
= 5.99 + 11.59 + 5.99
= 23.57 ft