Question

Write an equation for a cosine function with the

followingproperties.
amplitude = 2, period = /6, phase shift = /2.

Answer 1

The required function is
`f(x)=2\cos ((\pi)/(3)x-(2\pi)/(3))`.

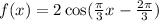Explanation:

Note: The value of period and phase shift are not given properly.

Consider amplitude = 2, period = 6, phase shift = 2.

The general form of cosine function is

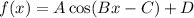`f(x)=A\cos (Bx-C)+D` ..... (1)

where, |A| is amplitude,
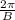`(2\pi)/(B)` is period, C/B is phase shift and D is midline.

From the given information we conclude that

`|A|=2`

`(2\pi)/(B)=6`

`(2\pi)/(6)=B`

`(\pi)/(3)=B`

`\text{Phase shift}=(C)/(B)`

`\text{Phase shift}* B=C`

`2* (\pi)/(3)=C`

`(2\pi)/(3)=C`

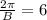
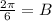
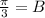
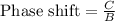
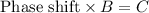
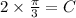
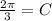
Substitute A=2,
`B=(\pi)/(3)` and
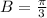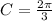`C=(2\pi)/(3)` and D=0 in equation (1).

`f(x)=2\cos ((\pi)/(3)x-(2\pi)/(3))+0`

`f(x)=2\cos ((\pi)/(3)x-(2\pi)/(3))`

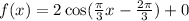
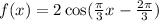
Therefore, the required function is
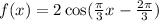`f(x)=2\cos ((\pi)/(3)x-(2\pi)/(3))`.