Question

Find the critical point of the function f(x) = x2 + 2x - 3.

(1, 4)

(-1, -4)

(-1, 4)

(1, -4)

Answer 1

(-1, -4)

Explanation:

The critical point is the point where the slope is 0 or undefined.

This is a parabola (quadratic), so there wont be any undefined points, only a critical point where slope is 0.

We need to take the derivative of the function and set it equal to 0 to find the x coordinate of the critical point. Then we plug in that x point into original equation to find the y coordinate.

Lets see the power rule of differentiation before we differentiate this function.

Power Rule:
`(d)/(dx)(x^n)=nx^(n-1)`

Also, differentiation a constant is always 0!!

Now, differentiating:

`f(x)=x^2+2x-3\\(d)/(dx)(f(x))=2x+2`

Now, we set equal to 0 and find x:

`2x+2=0\\2x=-2\\x=(-2)/(2)\\x=-1`

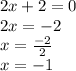
Now, we find y:

`f(x=-1)=(-1)^2+2(-1)-3=-4`

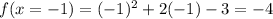
So,

x = -1

y = -4

The critical point is (-1, -4)