Answer:
Please find the attachment.
Explanation:
We are asked to explain why
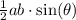 gives the area of a triangle with sides a and b and included angle theta.
gives the area of a triangle with sides a and b and included angle theta.
We know that area of a triangle is equal to half the product of base and height of the triangle.
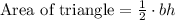
Upon looking at our given triangle, we can see that the base of the triangle is equal to 'a'.
The height of the triangle can be determined using sin(theta) as sine relates opposite side of right triangle with its hypotenuse.
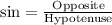

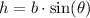
Upon substituting our given values in area formula, we will get:
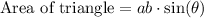
Hence, proved.