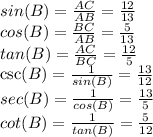Question

Suppose that

is a right triangle with
.

If AB = 13 and BC = 5, compute the values of the six
trigonometricfunctions of angle B.

Answer 1

sin(B) = 12/13

cos(B) = 5/13

tan(B) = 12/5

csc(B) = 13/12

sec(B) = 13/5

cot(B) = 5/12

Explanation:

If ABC is a right triangle, assuming that ∠C = 90°, then the segment AB =13 is the hypotenuse and the other two sides are:

`BC = 5\\AC = √(13^2 - 5^2)\\AC = 12`

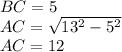
The six trigonometric functions of angle B are:

`sin(B) =(AC)/(AB)= (12)/(13)\\cos(B) = (BC)/(AB) =(5)/(13)\\tan(B) = (AC)/(BC) =(12)/(5)\\\csc(B) =(1)/(sin(B))= (13)/(12)\\sec(B) = (1)/(cos(B)) =(13)/(5)\\cot(B) = (1)/(tan(B)) =(5)/(12)\\`