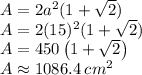Question

Find the area of an octagon whose perimeter is 120 cm.

Answer 1

The area of an octagon whose perimeter is 120 cm is 1086.4
`cm^(2)`

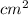
Explanation:

An octagon is a polygon with eight sides. If the lengths of all the sides and the measurement of all the angles are equal, the octagon is called a regular octagon.

There is a predefined set of formulas for the calculation of perimeter, and area of a regular octagon.

The perimeter of an Octagon is given by

`P=8a`

and the area of an Octagon is given by

`A=2a^(2)(1+√(2))`

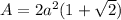
We know that the perimeter is 120 cm, solving for side length (a) in the perimeter formula we get

`120=8a\\(8a)/(8)=(120)/(8)\\a=15`

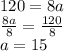
Now, we calculate the area

`A=2a^(2)(1+√(2))\\A=2(15)^(2)(1+√(2))\\A=450\left(1+√(2)\right)\\A\approx 1086.4 \:cm^(2)`