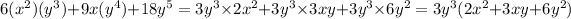Question

Factor each by factoring out the greatest common factor:

1. 10ab+5a
2. 3(????^3)ℎ−9(????^2)ℎ+12ℎ
3. 6(x^2)(y^3)+9x(y^4)+18y^5

Answer 1

1. Given expression,

`10ab + 5a`

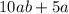
∵ 10ab = 2 × 5 × a × b,

5a = 5 × a

So, GCF(10ab, 5a) = 5a,

We can write,

`10ab + 5a=5a* 2b + 5a = 5a(2b+1)`

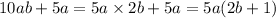
2. Given expression,

`3(x^3)h-9(x^2)h+12h`

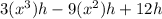
∵ 3(x³)h= 3 × x × x × x × h,

9(x²)h = 3 × 3 × x × x × h

12h = 2 × 2 × 3 × h

So, GCF(3(x³)h, 9(x²)h, 12h ) = 3h,

We can write,

`3(x^3)h-9(x^2)h+12h=3h* x^3 - 3h* 3x^2+3h* 4= 3h(x^3-3x^2+4)`

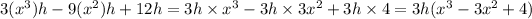
3. Given expression,

`6(x^2)(y^3)+9x(y^4)+18y^5`

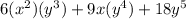
∵ 6(x²)(y³) = 2 × 3 × x × x × y × y × y,

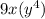`9x(y^4)` = 3 × 3 × x × y × y × y × y

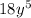`18y^5` = 2 × 3 × 3 × y × y × y × y × y

So, GCF(
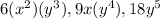`6(x^2)(y^3),9x(y^4), 18y^5`) = 3y³,

We can write,

`6(x^2)(y^3)+9x(y^4)+18y^5=3y^3* 2x^2 + 3y^3* 3xy+3y^3* 6y^2 = 3y^3(2x^2+3xy+6y^2)`