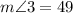Answer:
The complete demonstration would be
We know that line m and line n are parallel, also
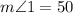 and
and
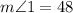 , line s bisects
, line s bisects
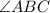 .
.
Now, by angle addition postulate we know that
 DEF=
DEF=
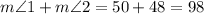
Then, by alternate exterior angle
 DEF
DEF
 , because alternate exterior angles are always congruent.
, because alternate exterior angles are always congruent.
So, by definition of bisector Angles 4 and 5 are congruent, because a bisector line divides the angle in two equal parts.
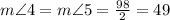
Then, we see that angle 3 and angle 4 are vertical angles, and the congruence postulate states that vertical angles are always congruent. So, by substitution we have