For starter, recall that an arithmetic progression
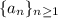 is given recursively by
is given recursively by
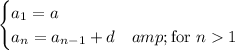
We can solve this explicitly for
 in terms of
in terms of
 :
:
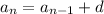
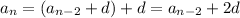
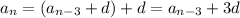
and so on, down to
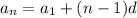
More generally, we can express
 in terms of an arbitrary term
in terms of an arbitrary term
 :
:
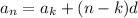
(notice how the index of
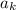 and the coefficient of
and the coefficient of
 on the right side add to
on the right side add to
 )
)
Let
 be the
be the
 -th term of this particular progression. We're given
-th term of this particular progression. We're given
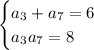
from which it follows that
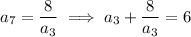
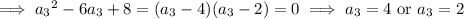

If
 , it follows that
, it follows that
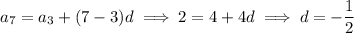
Otherwise, if
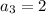 , then
, then
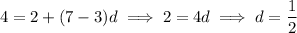
The sum of the first
 terms of an arithmetic progression
terms of an arithmetic progression
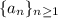 is
is
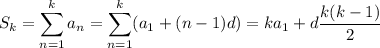
If
 , then
, then
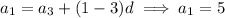
so that
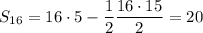
Otherwise, if
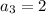 , then
, then
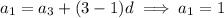
so that
