Question

Show that rigid body rotation near the Galactic center is consistent with a spherically symmetric mass distribution of constant density.

Answer 1

To solve this problem we will use the concepts related to gravitational acceleration and centripetal acceleration. The equality between these two forces that maintains the balance will allow to determine how the rigid body is consistent with a spherically symmetric mass distribution of constant density. Let's start with the gravitational acceleration of the Star, which is

`a_g = (GM)/(R^2)`

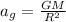
Here

`M = \text{Mass inside the Orbit of the star}`

`R = \text{Orbital radius}`

`G = \text{Universal Gravitational Constant}`

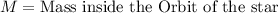
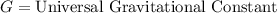
Mass inside the orbit in terms of Volume and Density is

`M =V \rho`

Where,

V = Volume

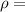`\rho =`Density

Now considering the volume of the star as a Sphere we have

`V = (4)/(3) \pi R^3`

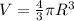
Replacing at the previous equation we have,

`M = ((4)/(3)\pi R^3)\rho`

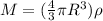
Now replacing the mass at the gravitational acceleration formula we have that

`a_g = (G)/(R^2)((4)/(3)\pi R^3)\rho`

`a_g = (4)/(3) G\pi R\rho`

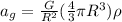
For a rotating star, the centripetal acceleration is caused by this gravitational acceleration. So centripetal acceleration of the star is

`a_c = (4)/(3) G\pi R\rho`

At the same time the general expression for the centripetal acceleration is

`a_c = (\Theta^2)/(R)`

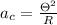
Where
`\Theta` is the orbital velocity

Using this expression in the left hand side of the equation we have that

`(\Theta^2)/(R) = (4)/(3)G\pi \rho R^2`

`\Theta = ((4)/(3)G\pi \rho R^2)^(1/2)`

`\Theta = ((4)/(3)G\pi \rho)^(1/2)R`

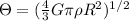
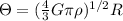
Considering the constant values we have that

`\Theta = \text{Constant} * R`

`\Theta \propto R`

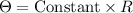
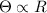
As the orbital velocity is proportional to the orbital radius, it shows the rigid body rotation of stars near the galactic center.

So the rigid-body rotation near the galactic center is consistent with a spherically symmetric mass distribution of constant density