Question

I posted this 2 hours ago can someone pls help?

a gallon of paint will cover about 400 square feet in a single coat. to the nearest tenth, how many gallons will be required to cover a circular region with a radius of 40 feet?

Answer 1

To find out how many gallons of paint are required to cover a circular region with a radius of 40 feet, calculate the area of the circular region using the formula A = πr². Then, divide the area by the coverage rate of one gallon of paint (400 square feet per gallon) to determine the number of gallons required.

Step-by-step explanation:

To find out how many gallons of paint are required to cover a circular region with a radius of 40 feet, we first need to calculate the area of the circular region. The formula for the area of a circle is A = πr², where A is the area and r is the radius. In this case, the radius is 40 feet, so the area is A = π(40)². We can use the approximation π ≈ 3.14 to calculate the area.

The area is A ≈ 3.14(40)² = 3.14(1600) = 5024 square feet. Now, we divide the area by the coverage rate of one gallon of paint, which is 400 square feet per gallon. So, the number of gallons required is 5024 / 400 ≈ 12.6 gallons to the nearest tenth.

Answer 2

0.314 gallon is required to cover a circular region with a radius of 40 feet

Step-by-step explanation:

Given

a gallon of paint will cover about 400 square feet in a single coat

To Find:

Number of gallons required to cover a circular region with a radius of 40 feet = ?

Solution:

Step 1: Finding Area of the circular region

The area of the circular region, A =
`\pi r^2`

where r is the radius

Now substituting r = 40 , we get

A =
`\pi * 40`

`A = 125.6 ft^2`

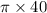
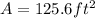
Step 2: Finding the number of gallons of paint required

To cover 400 sq feet = 1 gallon

so to cover 1 square feet =
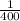`(1)/(400)`gallon

Now to cover 125.6 ft we need

`125.6 * (1)/(400)`

`(125.6)/(400)`

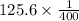
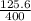
=> 0.314 gallon