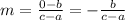Question

Thank you for your help!

Kim-Ly is writing a coordinate proof to show that the midpoints of a quadrilateral are the vertices of a parallelogram. She starts by assigning coordinates to the vertices of quadrilateral RSTV and labeling the midpoints of the sides of the quadrilateral as A, B, C, and D.

Answer 1

To find all coordinates, we just need to observe the graph.

The coordinates of point C are (2c,d). From the graph, we notice that the x-coordinate of C is the same x-coordinate of V, because they are in the same vertical lines.

The coordinates of point D are (c,0). The problem states that D is a mid point, so basically its coordinate is half of point's V, which is c.

The slope of both AB and DC is d/c. The slope is the fraction between y-coordinate and x-coordinate. If you we calculate the slope of DC, we would have d as vertical coordinate and c as horizontal coordinate.

The slop of both AD and BC is -b/c-a. The slope between the points A(a,b) and D(c,0) is

`m=(0-b)/(c-a)=-(b)/(c-a)`

Answer 2

See attached picture.

For the slope, the slope is the change in Y over the change in X.